Stochastisches Modell
Das stochastische Modell ist stets auch das Abbild einer stochastischen Wirklichkeit, die man in der einfachen Sprache der Mathematik einen stochastischen Prozeß nennt. Während die Bundesbahn einen hohen Aufwand treibt, um aus ihrem Fahrbetrieb eine möglichst determinierte Maschine zu machen - der Fahrplan ist der Prototyp eines deterministischen Modells -, ist andererseits das Verkehrsministerium heftig bestrebt, den stochastischen Prozeß "Straßenverkehr" möglichst reibungslos ablaufen zu lassen. Er bleibt aber dennoch stochastisch, weil jeder Verkehrsteilnehmer sein eigenes Ziel hat - so wie die Ameisen.
Es bedarf keines besonderen Hinweises, dass die stochastischen Prozesse am ehesten der Wirklichkeit entsprechen. Sie haben deshalb in der Mathematik auch einen festen Platz, den ihnen der russische Mathematiker Markoff zugewiesen hat. Ein Markoff-Prozeß zeichnet sich dadurch aus, dass seine zukünftige Entwicklung nur von der Gegenwart, nicht aber von der Vergangenheit bestimmt wird. (Ohne diese Einschränkung würden die Verhältnisse so kompliziert, dass man sie nur noch in Sonderfällen mathematisch behandeln könnte.)
Ist ein Straßenverkehr völlig regellos, so ist er ein stochastischer
Prozeß. Was kurze Zeit vorher noch über den Asphalt rollte, ist weg und hat keinen Einfluß auf das, was kommt. Anders ist es, wenn der Straßenverkehr stark von regelmäßig verkehrenden Omnibussen und Straßenbahnen bestimmt wird. Dann verliert er den Charakter eines Markoff-Prozesses, weil die durch den Fahrplan bedingte Verknüpfung dafür sorgt, dass die Vergangenheit des Systems auf die Zukunft Einfluß nimmt. In sehr vielen praktischen Fällen ist die Forderung dieser Unabhängigkeit unbedeutend oder nur so schwach gegeben, dass die Theorie der Markoffschen Prozesse, die übrigens immer noch einen relativ hohen mathematischen Aufwand erforderlich macht (B. Ferschl, "Zufallsabhängige Wirtschaftsprozesse - Grundlagen und Anwendung der Theorie der Wartesysteme", Wien und Würzburg 1964), dennoch brauchbare Aussagen liefert.
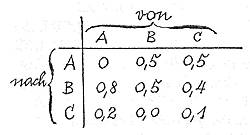
Sie befaßt sich ausführlich mit dem sogenannten "stationären Zustand" und sucht dessen Ursachen und Voraussetzungen zu klären, wie wir ihn etwa bei unserem Ameisenhaufen gefunden haben. Der stationäre Zustand ist identisch mit einem Zustand stochastischen Gleichgewichts. Auch hier spielt eine Übergangsmatrix eine Rolle, die Übergangswahrscheinlichkeiten von einem Zustand in jeden andern untersucht. Wichtig ist, dass der Anfangszustand im Gleichgewichtszustand nicht mehr vorkommt. Es liegt auf der Hand, dass es nicht für jeden Anfangszustand einen besonderen stationären Zustand geben kann. Damit ist aber der Gleichgewichtszustand eine Aussage über das System, eine Aussage stochastischer Natur.
Praktische Beispiele für Markoff-Prozesse gibt es genügend. Den Straßenverkehr haben wir bereits erwähnt. Ein Straßenverkehr ist etwa dadurch charakterisiert, welche Warteschlangen vor Ampeln, an Kreuzungen und auch sonst auftreten. Dies gilt aber auch für Kunden, die durch einen Selbstbedienungsladen wandern, um sich dann vor der Ladenkasse zu schlängeln. Unsere Ameisen sind sicherlich ebenfalls frei von unbewältigter Vergangenheit und daher Objekte eines Markoff-Prozesses. Aber auch die Aufträge in einer Werkstatt erfüllen unter gewissen Voraussetzungen die Bedingungen eines solchen Prozesses.
Markoff entwickelte seine Theorie an einem interessanten Problem. Er untersuchte, ob es möglich ist, Texte mit Hilfe wahrscheinlichkeitstheoretischer Mittel zu untersuchen. Hier sieht die Übergangsmatrix etwa so aus, dass man nachforscht, mit welcher Wahrscheinlichkeit aus einem bestimmten Buchstaben in einem Text oder in einer Sprache ein anderer wird - wie häufig also etwa auf ein k ein e folgt. Es ist möglich, mit Hilfe eines Computers Markoff-Prozesse zu simulieren, die Buchstabenketten, also Text, erzeugen. Im folgenden ist eine Textprobe angegeben, die durch ein solches Verfahren gewonnen wurde. Dabei ist eine Übergangsmatrix zugrundegelegt, die aussagt, mit welcher Wahrscheinlichkeit auf vier gegebene Buchstaben jeder fünfte folgt, und zwar für einen Text aus Kants "Kritik der reinen Vernunft". Der Prozeß lieferte folgenden Text:
VON JENEM URTEILHAFTIG IST ETWA DER SOLCHE. ES NICHT EBEN ALLGEMESSELBST VORSTELLUNGEN, UND TEIL WIRD. ES ABER DASS ES IST. DEN KANN. WIRD EINDRUECKE ZUM BESTIMMT GEMEINER ERFAHRUNG ABGELEGTEN ALLEN, FINESTAENDERN NUR A PRIORI. (Siehe dazu auch H. J. Flechtner, "Grundbegriffe der Kybernetik - Eine Einführung", Stuttgart 1966, Seite 58 und 89; übrigens ein sehr lesenswertes Buch zur Vertiefung des Stoffes.)
Die angegebenen Beispiele demonstrieren, welche vielfältigen Situationen man mit Hilfe des Markoff-Prozesses beschreiben kann. Er ist ein wichtiges Mittel zur Bildung stochastischer Modelle. In der kybernetischen Literatur findet sich ein Beispiel, das sehr schön die Grundgedanken der Markoffschen Theorie wiedergibt. Wir skizzieren es nach der Darstellung in dem gerade erwähnten Buch von H. J. Flechtner.
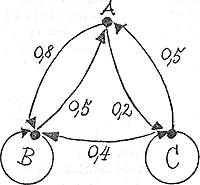
Gegeben ist ein Alphabet mit den drei Zeichen A, B und C. Die drei Zeichen treten auf mit den Wahrscheinlichkeiten
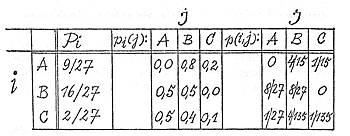
PA = 9/27, pB = 16/27 und pc = 2/27
Wie man sieht, sagen diese Zahlen noch nicht allzuviel. Nach der Shannonschen Formel ist der Informationsgehalt der Zeichen im Mittel, wenn man die Brüche dezimal darstellt: