(Die Zahlen in Klammern bedeuten: Dieser Prozentsatz bleibt in seiner Zone.)
Diese Matrix sagt jedem, der sich dafür interessiert, mit welcher Wahrscheinlichkeit irgendeine Ameise innerhalb von fünf Minuten von der einen Zone in die andere überwechseln wird.
Herr Klawuttke könnte die Matrix nun freilich noch unendlich verfeinern. Er brauchte dazu nur den hämischen Bemerkungen seines Fachkollegen nachzugeben und den Ameisenhaufen nebst Umgebung in 17 000 oder noch mehr Zonen zu teilen und dort in winzig kleinen Zeitmomenten Ameisen zu zählen (wobei wir es Herrn Klawuttke überlassen müssen, dafür ein geeignetes Verfahren zu finden, das ihn nicht noch vor seiner Habilitierung dem Wahnsinn anheim gibt). Bringt er es aber fertig, mit nahezu unendlich vielen Zonen und beinahe unendlich kleinen Zeitabständen zu operieren, so gerät unser Ameisenforscher allmählich in den Bereich mathematischer "Grenzwerte". Es könnte durchaus sein, dass sich beim Arbeiten mit unendlich kleinen Zonen und unendlich kleinen Zeiteinheiten feste Werte herausbilden - eben die "Grenzwerte". Möglicherweise kann Herr Klawuttke dann für jeden Punkt des Ameisenhaufens und seiner Umgebung sagen, mit welcher Wahrscheinlichkeit sich dort wie viele Ameisen aufhalten werden.
Dies, lieber Leser, ist eine verrückte, aber durchaus wissenschaftliche Idee.
Machen wir weiter mit unseren Phantastereien! Lassen wir Herrn Klawuttke die zahllosen Zonen aus der realen Welt des Ameisenvolkes mit Bleistift und Zentimetermaß auf eine glatte, ebene Stecktafel übertragen. Er geht dabei sehr sorgfältig vor. Dann steckt er in jede Zone eine lange Nadel. Und das macht er noch genauer; er steckt jede Nadel unterschiedlich tief ein. Die Nadeln ragen jeweils so hoch aus der Tafel, dass die Höhe ihres Köpfchens die Zahl der Ameisen in der betreffenden Zone angibt.
Auf diese Weise entsteht auf der Platte ein "Wahrscheinlichkeitsgebirge", eine wellig-hügelige Landschaft aus Stecknadelköpfchen. Sie ist nichts anderes als ein statistisches Modell des Ameisenhaufens.
Ein Modell? Ah so, richtig. Wir sind schon wieder mitten in unserer Kybernetik. Und Sie haben jetzt einen Einblick, welche Mühe sich die Wissenschaft gibt, um brauchbare Modelle für ihre Untersuchungen herzustellen.
Der erfundene Ameisenhaufen ist nun freilich ein Beispiel, das ob der Mühe, die sich der erfundene Forscher Klawuttke gibt, zunächst reichlich absurd erscheint Aber täuschen Sie sich nicht: Auf manches wissenschaftliche Modell wird noch weit, weit mehr Mühe und Gehirnakrobatik verwandt!
Auch wir wollen Klawuttkes Modell noch ein bißchen verfeinern. Wie wäre es, wenn wir es beweglich machten? Am besten, wir vollautomatisieren es so, dass die Nadeln sich von selbst mehr oder weniger weit aus der Platte herausbewegen können - je nachdem, wieviel Ameisen sich gerade in den betreffenden Zonen befinden. Unser Modell würde uns dann stets genauesten Aufschluß darüber geben, was die Ameisen gerade tun.
Freilich; Die Ameisen können so viel hin- und herrennen, wie sie wollen - solange sie immer gleichmäßig über die Zonengrenzen wechseln, solange also in jede Zone so viele neue Ameisen kommen, wie daraus entlaufen, solange bewegt sich das Modell nicht. Der Ameisenhaufen zeigt dann - trotz regstem Hin und Her - einen "stabilen Zustand".
Ist Herr Klawuttke aber so nett, den Tierchen einen Fleischbrocken hinzuwerfen, so entsteht Aufruhr im Ameisenhaufen. Ein bestimmter Prozentsatz der Ameisen begibt sich, ohne an das Arbeitssoll oder die soldatische Pflichterfüllung auch nur einen Gedanken zu verschwenden, eilends zum Mahle. Unser Modell zeigt das sofort an. Es bewegt sich heftig, macht dabei die Bewegungsströme deutlich und stellt sich schließlich auf einen neuen stabilen Zustand ein, bei dem man nur in der Gegend des Fleischbrockens eine deutliche Erhöhung im Nadelgebirge feststellt: Hier haben sich besonders viele Ameisen versammelt.
Dieser Zustand dauert so lange an, bis das Fleisch gefressen ist. Dann gerät das Modell wieder in Bewegung, bis - so jedenfalls hoffen wir im Interesse des Ameisenvolkes - der vorherige stabile Zustand wiederhergestellt ist.
Von Phantastereien und Wahrscheinlichkeiten
Forscher Klawuttke ist nämlich auf ein neues Problem gestoßen. Er hat gemerkt: Bevor er überhaupt beginnen kann, sich über die Struktur des Ameisenhaufens Gedanken zu machen, muss er versuchen, möglichst exakt die Strukturelemente zu definieren. Er muss dabei, wenn er es wirklich ernst meint, so sorgfältig vorgehen, dass er nachher jeder Ameise, die er trifft, eindeutig nachweisen kann, zu welcher Elementengruppe sie gehört.
Das aber ist, wie jedermann zugeben wird, bei Ameisen nicht ganz einfach, zumal dort die Königin keine Krone trägt, der Soldat kein Gewehr und der Arbeiter keinen Blauen Anton.
Wenn sich Forscher Klawuttke also nicht auf die Unterscheidung zwischen lebendigen und toten Ameisen beschränken will (was wissenschaftlich zwar durchaus zulässig wäre, Klawuttke aber gewiß nicht binnen der nächsten fünf Jahre zum Professor der Ameisologie macht), so bleibt ihm nur übrig, eine Differenzierung der Strukturelemente zu ersinnen, die einerseits etwas Vernünftiges an den Tag bringt, andererseits aber von einem Menschen, der der Ameisensprache nicht mächtig ist, überhaupt praktiziert werden kann.
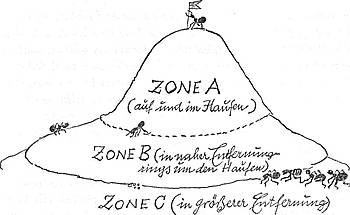
Was könnte er tun? Er könnte versuchen, das Problem ganz von außen her zu lösen. Beispielsweise, indem er den Scheitelpunkt des Ameisenhaufens als den Mittelpunkt zweier konzentrischer Kreise betrachtet. Der innere Kreis würde gerade den Haufen selbst umschließen, der zweite hätte den - sagen wir - doppelten Durchmesser. So könnte Klawuttke nun schon mit drei Elementengruppen operieren: Mit Elementen (auf deutsch: Ameisen)
A - auf und in dem Haufen ( = innerhalb des inneren Kreises)
B - in naher Entfernung rings um den Haufen (= zwischen
innerem und äußerem Kreis)
C - in größerer Entfernung ( = außerhalb des äußeren Kreises).
Gewiß kann man darüber streiten, ob diese Einteilung sinnvoll ist.
Zweifellos wird eines Tages ein Fachkollege dem Forscher Klawuttke vorwerfen, er sei ein unseriöser und unwissenschaftlicher Ignorant (worauf Klawuttke von der Universität seiner Heimatstadt spontan zum Honorarprofessor ernannt wird) und hätte statt der drei "Zonen" (so nennt man die abgeteilten Gebiete) sieben, siebzehn oder siebzigtausend nehmen müssen.
Das soll uns aber zunächst nicht anfechten. Uns ist Forscher Klawuttkes Methode gerade recht, und wir wollen uns darum jetzt mit ihm über die Kreise beugen, um die Ameisen zu zählen, die dort herumwimmeln.
In jedem Bezirk machen wir eine Volkszählung. Außerdem halten wir fest, wie viele Ameisen im Zeitraum von fünf Minuten von der einen Zone in eine andere wandern. (Und weil wir uns alle miteinander nicht verhehlen, dass solche Zählungen gerade bei Ameisen ein verhältnismäßig scharfes Auge und einen sehr geschulten Blick verlangen, sind wir froh, dass wir es hier nur auf dem Papier tun müssen.)
Zunächst interessiert uns vor allem die Wanderung der Ameisen von Zone zu Zone. Und auch da sind uns die absoluten Zahlen nicht so wichtig; auf eine Ameise hin oder her soll es uns nicht ankommen. Wir geben uns mit Prozentzahlen zufrieden. Die halten wir in einer sogenannten "Übergangsmatrix" fest: