Nach diesen tröstlichen Beispielen von menschlicher und maschineller Unvollkommenheit könnten wir noch schnell einen Blick ins Gebiet des Vollkommenen tun - schauen wir bei der Mathematik vorbei! Diese Disziplin kann man ja geradezu als eine Sammlung kybernetischer Modelle betrachten. Rückkopplungsvorgänge beispielsweise lassen sich dort durch Differentialgleichungen darstellen. Wer genügend von Mathematik versteht, wird wissen, wie die Zusammenhänge liegen. An den Lösungen dieser Gleichungen kann man genau studieren, wie und warum sich Schwingungen aufbauen. Und man sieht ihnen (wenn man den mathematischen Blick hat) auch an, unter welchen Voraussetzungen die Schwingungen zur Selbstzerstörung des Systems führen können.
Noch ein bißchen Wissenschaft - aber ohne Mathematik? Gut, dafür mit Wintersport.
Stellen Sie sich einen Skihang vor und einen Lift, der hinaufführt! Die Abfahrt ist nicht einfach und ziemlich schmal. Schon oft gab es Unfälle, und deshalb wurde vorgeschrieben, dass sich nur eine bestimmte Zahl von Skifahrern auf dieser Abfahrt tummeln darf. Dem Mann am Skilift wurde aufgegeben, dafür zu sorgen, dass diese Zahl nicht überschritten wird.
"Und wia mach i denn dös?" fragt der Liftsepp bieder. "Ganz einfach", sagt ihm der Kurdirektor, "laß nur so viele mit dem Lift hinauf, wie runterfahren dürfen!" In den frühen Tagesstunden ist das kein Problem. Nur alle paar Minuten kommt ein Skifahrer und will hinauf. Der Sepp kennt sie alle, er weiß, wer gerade mit dem Lift nach oben fährt und wer nach einiger Zeit am Fuß der Abfahrt wieder landet. Das System ist - und nun kommt der wissenschaftliche Ausdruck, um den es uns geht - "deterministisch". Zu deutsch: es ist überschaubar und ohne großen Aufwand zu regeln.
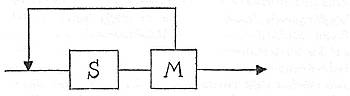
Anders geht es zu, wenn am Nachmittag der große Ansturm auf den Lift einsetzt. Jetzt ist es mit dem souveränen Überblick nicht mehr getan. Nun hilft nur noch eine Methode, die sich der Sepp vom Herrn Lehrer hat ausarbeiten lassen. Er regelt sein System, indem er zählt, wieviel Leute mit dem Lift hinauffahren (Größe I) und wieviel unten an der Abfahrt ankommen (Große II). Die Differenz ist seine Regelgröße; mit ihr steuert er die Beschickung seines Lifts. Ist II größer als I, kann er seine Liftsessel getrost für jeden Interessenten offenhalten. Wird aber I größer als II, so muss er achtgeben und den Drang nach oben bremsen. Ein solches System, bei dem der genaue Überblick dahin ist und man nur noch mit Zählen oder Messen durchkommt, also mit rein statistischen Methoden, nennt man "stochastisch".
Unser Ameisenforscher Klawuttke zum Beispiel konnte in seinem Ameisenhaufen auch nur mit Hilfe der Stochastik vorgehen, der "Zufallsrechnung".
Übrigens gibt es keinerlei objektiven, allgemeingültigen Maßstab, ob ein System deterministisch oder stochastisch ist. Für ein Genie mit phantastischer Beobachtungsgabe mag die Mehrzahl aller Systeme, die dem Durchschnittsbürger stochastisch erscheinen, durchaus noch deterministisch sein. Und wenn man genau wüßte, wie der Wunderhund Lassie vom Fernsehen die Dinge wirklich sieht, so würde man vermutlich feststellen, dass für ihn jedwedes System stochastisch ist. Oder gerade nicht? Wer weiß!
Finden Sie nicht auch, dass es erstaunlich ist, wo wir mit unserem simplen Rückkopplungsmodell überall hingeraten sind?

Das eben ist ja das Bezeichnende an der Kybernetik, dass ein einziges Modell so viele Tatbestände zu erklären vermag.
Nun ist es in Wirklichkeit nicht so, dass Rückkopplungssysteme so vereinzelt aufzutreten pflegen, dass man sie allein und für sich genau beobachten und studieren kann wie die Schaustücke im Museum. Meist sind viele von ihnen zu hochkomplexen Systemen verbunden ("vermascht" sagen die Wissenschaftler, denen komplizierte Strickmuster nicht fremd sind), und es wird dann oft sehr schwer, zutreffende Modelle zu entwerfen.
Wir müssen jetzt auch in aller Offenheit eingestehen, dass die im vorhergegangenen Kapitel aufgezeigten Modelle, bei denen es um reine Steuerungsvorgänge ohne Rückkopplung ging, sehr selten sind. Die Kochtopffabrik zum Beispiel, die wir da zeigten, wird wohl nur in der Vorstellung eines autokratischen und auch sonst geistig beschränkten Direktors ein reiner Steuerungsbetrieb sein; ohne Rückwirkungen von unten in hohe und höchste Stellen kann kein moderner Betrieb existieren. Durch jeden gesunden Industriebetrieb ziehen sich, dichtgewebte Stränge von Rückkopplungsverbindungen: Die Direktion wird sich von ihren Abteilungen Berichte geben lassen und daraufhin ihre Direktiven ändern; die Einkaufsabteilung wird sich den Vorstellungen der Techniker anzupassen suchen; andererseits wird sie hier und da auch die Techniker davon überzeugen müssen, dass deren Vorstellungen von der Güte des Kochtopfblechs weltfremd sind.
Auch die Schreinerei von Meister Holzbock weist zahlreiche Rückkopplungsmechanismen auf, wenn sie richtig betrieben wird: Bretter durchlaufen so lange die Hobelmaschine, bis die Dicke auf den Viertelmillimeter genau ist; von der Bandsäge schallen herbe Kommentare dorthin, wo die Schnittstellen aufgezeichnet, aber offenbar nicht korrekt vermerkt werden; und der Meister selbst rechnet Tag und Nacht, um aus dem Ausstoß seiner Werkstatt zu ermitteln, wie, wann und zu welchem Preis er neues Holz einkaufen muss.
Ja, sogar unser Gesangverein ist ein Gewirr von Rückkopplungssystemen - wie das immer und überall der Fall ist, wo Menschen im Spiel sind. Dass Herr Brüllmann zurücksteckt, wenn er in seinen Angriffen auf den Vorsitzenden zu weit gegangen ist; dass andererseits der Vorsitzende seine einsamen Entschlüsse vorsichtiger faßt, sobald er bemerkt, dass er eine Front gegen sich hat - all das geht auf dem Wege der Rückkopplung vor sich, und leider sind hier die Teilsysteme längst nicht so leicht durchschaubar wie die Sandschaufelei von Paul, Antonio und Emil.
Denn dummerweise sind Menschen im allgemeinen keine deterministischen, sondern überaus stochastische Systeme. Das macht den Umgang mit ihnen so problematisch.