Wenn wir so weitermachen, die Änderungsmöglichkeiten von einem Zustand in einen anderen nicht mehr als selbstverständlich nehmen, sondern nur noch als wahrscheinlich; wenn wir nur noch in Prozenten angeben, in wie vielen aller Fälle der Übergang wohl stattfinden wird...
Nun, dann haben wir bald eine Matrix, die mit ihren geteilten, gebrochenen Werten unserer ersten Ameisenmatrix ähnelt, in die Forscher Klawuttke eingetragen hatte, wie viele Tierchen vom Zentrum des Haufens zur Peripherie zu eilen pflegen. Erinnern Sie sich? Beidesmal handelt es sich um die Matrizen von sogenannten "stochastischen Maschinen". Das ist das genaue Gegenteil von "determinierten Maschinen". Bei einer determinierten Maschine weiß man im voraus immer ganz genau, was passieren wird - bei einer stochastischen nur ungenau oder überhaupt nicht. Die in der Matrix eingetragenen Werte stellen sich dort erst einigermaßen genau ein, wenn man lange genug beobachtet hat. So wollen es die Gesetze der Wahrscheinlichkeit.
Ein Tischtennisball, der bei windstillem Wetter vom Schiefen Turm zu Pisa fällt, ist eine determinierte Maschine. Man kann vorher ausrechnen, wo er aufprallen wird und wann er unten ankommt. Ein Tischtennisball jedoch, der über das Deck eines schlingernden Schiffes rollt, ist eine stochastische Maschine. Kein Mensch würde sich getrauen, vorauszusagen, welche Richtung er als nächstes nimmt.
Streng fahrplanmäßiger Eisenbaheverkehr ist eine determinierte Maschine, der Autoverkehr in einer Großstadt eine stochastische. Das sagten wir bereits.
Es gibt Grenzfälle. Der Tischtennisball, den man auf die Platte fallen und dort hüpfen läßt, ist eigentlich eine determinierte Maschine. Nach Aufsprungwinkel, Reibung, Verformungskoeffizient und einigen weiteren physikalischen Größen ließe sich sein Hüpfen im Vorhinein genau berechnen und sogar planen. Aber das tut natürlich niemand. Deshalb kann man einen solchen Ball nur stochastisch betrachten.
Die Zahl der Grenzfälle ist vermutlich größer als die Menge der rein deterministischen oder rein stochastischen Maschinen. Zum Beispiel steckt in der besten automatischen Bohrmaschine - die an sich doch streng deterministisch ist - ein stochastisches Element: Der Bohrer kann - irgendwann - abbrechen. Auch viel Subjektives spielt mit. Während dem Astronomen die Bewegung der Himmelskörper als das faszinierendste Beispiel einer determinierten Maschine gilt, ist dem Laien das Durcheinander am gestirnten Himmel über sich die schiere Stochastik.
Wenden wir uns zurück zur strengen Mathematik? Gut.
Von stochastischen und determinierten Maschinen
Nachdem wir Sie nun schon so weit ins Abstrakte geführt haben, vergessen Sie die Bohrmaschine am besten wieder. Sie diente uns nur als ein ganz grobes Beispiel für eine determinierte Maschine. Viel lieber wäre es uns, wenn Sie jetzt den Begriff "Maschine" ganz abstrakt denken würden. Als System vielleicht, als Modell, unseretwegen als Programm für einen Computer.
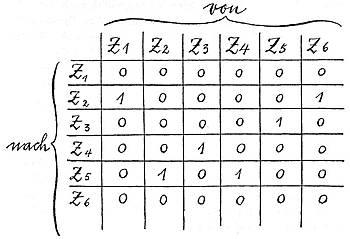
Für einen solchen simpel programmierten Computer könnte zum Beispiel folgende Matrix gelten:
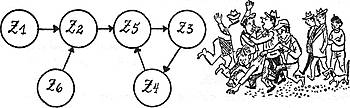
Von Z1 aus stellt sich also Z2 ein, dann Z5, drauf Z3, schließlich Z4, nun wieder Z5. Anschließend geht es im Zyklus Z3-Z4-Z5 weiter.
Diesen Zyklus, der endlos dauern kann, nennt man das "Gleichgewicht", den Weg über Z1 und Z2 aber den "Einschwingvorgang".
Erinnern Sie sich? Als von Meister Klawuttkes Ameisen die Rede war, haben wir uns eingehend über Einschwingvorgänge und stabile Gleichgewichte unterhalten. Hier sehen Sie nun, wie man derartige Vorgänge als Graphen darstellt. Darum kann der Graph, den wir eben gezeigt haben, genauso als Modell für Klawuttkes Ameisenbewegung gelten.
Was sagen Sie dazu?
Sicher erinnern Sie sich auch noch an Klawuttkes hinterlistigen Versuch, den Ameisenhaufen in Aufruhr zu bringen, indem er zweitausend sechsbeinige Genossen herausfing und in eine Zigarrenkiste steckte. Das Ameisenvolk verfiel minutenlang in Panik, fing sich dann aber wieder.
Als Klawuttke die gefangengehaltenen Ameisen wieder zu den ihren entließ, gab es erneut ein entsetzliches Durcheinander - aber wieder nur kurz. Dann zeigte das Ameisenvolk von neuem sein gewohntes, planmäßig krabbeliges Bild.
Nun, bitteschön, genau das sagt ja. unser Graph aus!
Fängt Klawuttke das Regiment Ameisen heraus, so tritt Zustand Z1 ein: Ein Umschwingvorgang beginnt, der stracks zur Stabilität bei Z3-Z4-Z5 führt.
Und was, wenn der Forscher die Schachtel der Gefangenen wieder öffnet? Dann wird das System künstlich in Zustand Z6 gebracht - aber über den Umschwingvorgang Z6-Z2 kehrt es ebenfalls wieder in sein Gleichgewicht zurück.
Das hört sich alles sehr schön und sehr logisch an, nicht wahr?
Nur ist es leider nicht ganz korrekt. Denn wir haben hier, um Ihnen das Problem auf dem einfachsten Weg zu zeigen, nur so getan, als wäre der Ameisenhaufen eine determinierte Maschine. In unserem Fall - bei Klawuttkes Experiment mit den herausgefangenen Tierchen - verhält er sich auch wirklich so. Deshalb war unser Versuch, den Ameisenhaufen mit dem Modell einer determinierten Maschine zu erklären, wenigstens nicht komplett falsch.
Zumeist jedoch kann man den Ameisenhaufen nicht so deterministisch nennen wie etwa eine Bohrmaschine. Die Tiere tun uns in der Regel nicht den Gefallen, sich streng nach Plan zu bewegen. Da spielt so vieles mit - Wetter, Feinde, ein Tannenzapfen, der in die Ameisenburg fällt -, dass es geradezu ein Wunder wäre, wenn unser simpler Graph das ganz und gar richtige Modell darstellte.
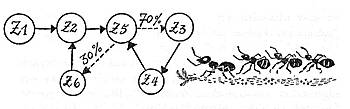
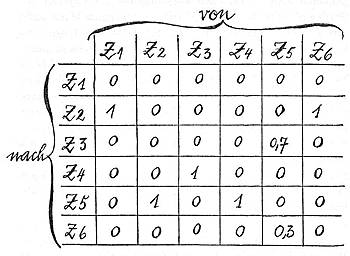
Wahrscheinlicher ist es, dass nur in - sagen wir - 70% aller Fälle Zustand Z5 in Zustand Z3 übergeht, also ein Gleichgewicht einkehrt. Mit dreißigprozentiger Wahrscheinlichkeit tritt nach Zustand Z5 wieder Z6 ein: Rückfall in Chaos, Anarchie, Panik und Protestmärsche.
In diesem Fall müßten wir einen anderen Graph zeichnen, und der würde dann etwa so aussehen, wie es unten dargestellt ist: Die Prozente sind besonders vermerkt.