Die Stadt Toronto hat eine Verkehrssteuerungsanlage, schon seit 1963. Etwa tausend Kreuzungen mit ihren rot-grün-gelben Ampeln sind angeschlossen. Kontakte im Boden zählen unermüdlich die darüberrollenden Kraftfahrzeuge und liefern ihre Daten an den Elektronenrechner. Der konzipiert daraus eine beständig wechselnde Verkehrsstrategie: Gibt jetzt diesem Straßenzug grün und dann jenem, halt hier den Querverkehr zurück und beschleunigt dort durch aufmunternde Zeichen den Autofluß.
Das Arbeitsprinzip des Computers besteht nur darin, dass er im Innern seiner Magnetspeicher ein Modell der ganzen großen Stadt Toronto abgebildet hat, dort die realen Verhältnisse nachspielt und danach seine Entscheidungen trifft.
Schön ist, dass dieses Modell auch außerhalb der Wirklichkeit funktioniert. Man benützt es für Experimente. Zum Beispiel: Nun, sagen wir, die Stadtverwaltung will eine neue Schnellstraße aus der Nachbarstadt herüberziehen. Das teilt sie dem Computer mit und bittet ihn, doch mal schnell durchzuprobieren, wie sich das auf den Verkehrsfluß auswirken würde. Er tut's und gibt pflichteifrig Bescheid. Oder das städtische Bauamt muss wegen Kabelarbeiten eine wichtige Straße sperren. Was wird passieren? Der Computer spielt's durch, meldet, wo der Verkehr daraufhin zusammenbrechen wird, und erlaubt den Verkehrsplanern, so lange Umleitungsmaßnahmen zu treffen - immer noch am Modell! -, bis die Autos voraussichtlich wieder einigermaßen flott fahren können.
Nun haben wir ja schon mehrfach betont, dass die Computer üblicher Bauart nicht ein maßstäbliches Miniaturmodell dessen, was sie imitieren sollen, im Innern ihrer graulackierten Bäuche tragen. Wenn man den Roboter der Verkehrsregelung von Toronto öffnet, so findet man keine winzigen Straßen, Ampeln und Automodelle, sondern auch nur Spulen, Draht und Transistoren. Das Modell ist irreal, ist in die Mathematik entrückt worden, umgeformt in Zahlenreihen und Chiffren, die sich als elektrische Impulse im Computer verarbeiten und speichern lassen.
Moderne Kybernetik, so sagten wir einmal in dieser Publikation, ist im Grunde nichts anderes als die Mathematisierung von Vorgängen und Abläufen.
Auch dass wir in diese Mathematik hier nicht so richtig eindringen können, haben wir schon klargemacht. Sie entzieht sich eben leider der populären Darstellung. Deshalb können wir immer nur ein bißchen in den Grenzgebieten der Mathematik herumspazieren und über den Zaun schauen.
Das möchten wir auch jetzt wieder machen.
Zunächst wollen wir uns aber nicht mit so komplizierten Gebilden beschäftigen wie mit dem Straßenverkehr oder unserem Ameisenhaufen, sondern mit ganz schlichten sogenannten "determinierten Maschinen". Mit Maschinen also, deren logische Abläufe vorher festgelegt sind.
Nehmen wir zum Beispiel eine automatische Werkzeugmaschine, die mit vielen anderen an einer langen "Transferstraße" aufgereiht ist, wie man sie in den Autofabriken seit Jahren kennt. Die Werkstücke gleiten selbsttätig von Maschine zu Maschine weiter und werden dabei ohne menschliches Zutun bearbeitet.
Unsere Maschine, von der hier die Rede ist, kann einiges; sie ist fast schon ein ausgebildeter Mechaniker. In den nächsten drei Tagen werden jedoch nur Hinterachsen hergestellt; da braucht die Maschine lediglich eine Tätigkeit zu verrichten: Sie muss ein Loch in den Achskörper bohren. Nun hat jede solche Maschine eine Reihe von "Zuständen", die man mit Z1, Z2, Z3 und so weiter bezeichnen kann. Da ist Z1 zum Beispiel der Zustand "Werkstück vom Zulieferband rechts holen", Z3 "Werkstück auf der Spannvorrichtung justieren". Und so weiter.
Bei unserer Maschine sind diesmal nur drei Arbeitsvorgänge interessant. Das Werkstück, den Achskörper, bekommt sie von der Kollegin vor ihr bereits handgerecht auf die Arbeitsplatte geschoben. Ihr bleiben darum nur Z5 ("Bohrer einsenken"), Z7 ("Bohrer herausziehen") und Z12 ("Werkstück weiter transportieren") .
Als streng determinierte Maschine hält sie sich genau, an diese Reihenfolge: Z5, Z7, Z12 und wieder zurück nach Z5, dann erneut nach Z7... Und so weiter.
Die Maschine beschreibt in ihren Zustandsänderungen einen Zyklus. Sagt der Fachmann.
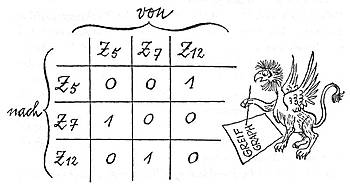
Um einen solchen Zyklus aufzuschreiben, kann man sich einer Form bedienen, die wir schon kennen: Man zeichnet eine Übergangsmatrix, wie Forscher Klawuttke sie seinen Ameisen zuliebe verfaßte. Bei unserer Werkzeugmaschine sieht diese Übergangsmatrix so aus:

Überall dort, wo ein Übergang von einem Zustand in den anderen stattfinden kann, soll und muss, wird eine Eins eingetragen - sonst eine Null.
Das Kennzeichen einer streng determinierten Maschine ist, dass in jeder senkrechten Spalte ihrer Übergangsmatrix nur eine einzige Eins steht. Wären es mehr, so hätte die Maschine ja die Wahl, welchen nächsten Zustand sie wählen darf, und das würde für die Autoproduktion eine Katastrophe bedeuten. Deshalb mag man sich in der Industrie auf andere als determinierte Maschinen nicht einlassen.
Hingegen gibt es die Möglichkeit, dass eine Maschine von mehreren Zustandsmöglichkeiten auf einen gemeinsamen Folgezustand überzugehen hat. Zum Beispiel, wenn sich von unserer Bohrmaschine zwei Zulieferbänder für die Achskörper vereinigen und sie sich die Werkteile von links oder rechts - mal so, mal so - zu greifen hat, um sie dann in der gewohnten Weise zu bearbeiten und weiterzugeben.
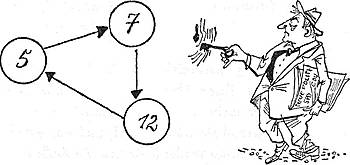
Aber so kompliziert wollen wir's im Augenblick noch gar nicht anstellen. Lieber möchten wir Ihnen eine andere Darstellungsmöglichkeit für den Zyklus Z5, Z7, Z12 angeben. Keine Matrix diesmal, sondern einen Graph. Das klingt nach dem Vogel Greif und sieht ein bißchen wie ein komischer Vogel aus. Aber das Wort kommt nicht aus der Ornithologie, sondern aus dem Griechischen, und zwar aus dem gleichen Stamm wie die "Graphik" und der "Fotograf". Es heißt schlicht "Geschriebenes" oder "Gezeichnetes".
Für unsere Zwecke brauchen wir einen "dynamischen Graph". Er kommt zustande, indem man jedem Zustand einen Punkt zuteilt und die Punkte, zwischen denen ein Übergang möglich ist, durch wohlgestaltete Pfeile verbindet. Der dynamische Graph unserer Bohrmaschine würde also so aussehen: