Aus dieser Tabelle kann man mehr entnehmen als nur die eingetragenen Werte, wenn man weiß, dass gilt:
Logarithmen
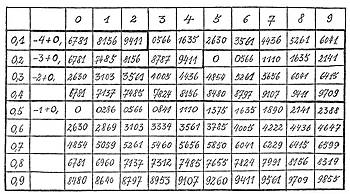
Für die Freunde von Zahlen haben wir hier eine kleine Tabelle von Logarithmen zur Basis 2 abgedruckt. Sie geht von 0,1 bis 0,99. Man liest sie so, dass man etwa für 0,46 in die Zelle für 0,4 geht und unter Spalte 6 die Ziffernfolge 8797 findet. Wie man in der zweiten Spalte abliest, hat dann der Logarithmus den Wert
-2 + 0,8797 = -1,1203
In der Tabelle ist also die Ziffernfolge eingetragen, die man dem entsprechenden Rumpf in Spalte 2 anfügen muss. Dabei springt allerdings die Zuordnung entsprechend den dicken Balken.
| lb(a.b) | = | lb(a)+lb(b) |
| lb(a/b) | = | lb(a)-lb(b) |
| lb(an) | = | n lb(a) |
| lb(l) | = | 0 |
| lb(2) | = | 1 |
| lb(4) | = | 2 |
| lb(8) | = | 3 |
Wir berechnen daraus den Binälrlogarithmus für 10. Es ist laut Tabelle lb(0,l) = -4 + 0,6781
Nun ist aber auch 0,1 = 1/10, und damit gilt
Ib(l/10) = lb(l) -lb(10) = -4 + 0,6781= -3,3219
Daraus entnimmt man, dass gilt - da lb (1) =0 ist - :
-lb(10) =-3,3219 oder lb(10) = 3,3219
Will man nun etwa den Logarithmus für 0,08 errechnen, der in der Tabelle nicht mehr vorkommt, so ist 0,08 = 0,8/10 oder lb(0,08)=lb(0,8)-lb(10)
lb (0,08) = -1 + 0,6781 - 3,3219 = - 3,6438
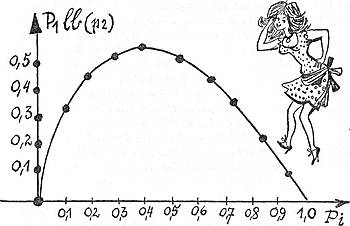
Leicht errechnet man sich ans dieser Tabelle auch eine entsprechende Tabelle für die Form - p.ln(p), wie sie in der Shannonschen Formel auftritt. Diese Funktion hat folgenden Verlauf:
Und dazu gehört folgender Kurvenverlauf: