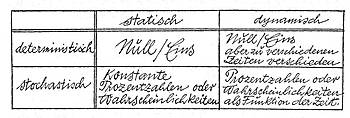
Rechts unten in der Tabelle steht das allgemeinste von einer Übergangsmatrix erfaßte Modell; es ist stochastisch und dynamisch.
Wie wir später sehen werden, kann man mit Übergangsmatrizen Automaten - wie etwa Computer - beschreiben, aber auch viele Vorgänge im Gehirn, so dass diese Technik, zusammen mit der Graphentheorie, ein wirkungsvolles kybernetisches Instrument ist. Ihre Behandlung gehört in den Bereich der mathematischen Kybernetik, ihre Anwendung liegt im Bereich der allgemeinen Kybernetik.
Übergangsmatrix
Die hier verwendete Übergangsmatrix spielt vor allem in der von Ross Ashby ("An Introduction to Cybernetics", London) entwickelten, sehr methodischen Kybernetik eine bedeutsame Rolle zur Charakterisierung des Verhaltens von Systemen (gelegentlich auch "Maschinen" genannt). Man geht davon aus, dass ein solches System ein Verhalten aufweist und sein Verhalten ändert, also von einem Zustand in einen andern übergeht. Endliche Systeme verfügen über endlich viele Zustände.
Schreibt man sich in einer solchen Matrix horizontal und vertikal alle Zustände an, so kann man auf den Kreuzungspunkten eintragen, ob von einem horizontalen Zustand auf einen vertikalen Zustand übergegangen werden kann (Die Eintragung ist dann eine 1) oder nicht (dann findet sich eine Null). Damit kann man Systeme klassifizieren, denn alle Systeme mit derselben Matrix weisen ein gleiches Verhalten auf - auch wenn man ein solches Verhalten, je nach Art der Zustände, unterschiedlich interpretieren kann.
Solche Matrizen kann man wiederum durch Graphen darstellen, so dass auch von hier aus ein Zugang zur Graphentheorie gegeben ist. Jeder Zustand ist dort ein Punkt. Eine 1 bedeutet, dass zwei Punkte miteinander zu verbinden, sind. Führt der Weg von einem Zustand stets nur zu genau einem andern, so ist das System streng determiniert. Kann das System in eine stets gleichbleibende Folge von Zuständen gelangen - im zugeordneten Graphen wird das durch einen geschlossenen Zyklus deutlich -, so liegt ein Gleichgewichtszustand vor. Rückt man das System künstlich - also von außen - aus einem solchen Gleichgewichtszustand heraus und kehrt das System (auch nach einigen Umwegen) wieder in diesen zurück, so nennt man das Gleichgewicht "stabil". Rückt das System aber auf einen andern Gleichgewichtszustand, so war der alte Gleichgewichtszustand nur labil.
Die Folge der Zustände, bis ein Gleichgewicht eintritt, nennt man den Einschwing- oder Umschwingvorgang. Die Übergangsmatrix ist also tatsächlich ein Hilfsmittel zur Charakterisierung und Klassifizierung von Systemen aus ihrem Verhalten heraus. Die Frage nach dem Verhalten ist aber typisch kybernetisch. Ashby formuliert sinngemäß: "Kybernetik fragt nicht: Wie ist ein Ding? sondern: Was tut es, wie verhält es sich?"
Die Festlegung auf eine endliche Anzahl von Zuständen ist sehr oft eine Frage pragmatischen Vorgehens. Man wird sich dabei auf wesentlich viele Zustände beschränken.
Unendlich viele Zustände liegen etwa bei Meßwerten vor, wo alle Zahlen in einem Zahlenintervall auftreten dürfen. Der Zusammenhang zwischen einer Beschreibung mit endlich vielen und einer mit unendlich vielen Zuständen besteht dann etwa in einem Grenzwert. Oft liegen die Verhältnisse auch so, dass man zwar für eine bestimmte Klasse des Verhaltens eines Systems unendlich viele Zustände findet, dass diese aber mit unterschiedlicher Häufigkeit auftreten. Mit den Hilfsmitteln der Wahrscheinlichkeitsrechnung kann man dann gegebenenfalls endlich viele signifikante Zustände (Merkmale) finden, die eine endliche Betrachtung zulassen.
Während man im endlichen Fall Systeme, wenn sie determiniert sind, oft durch Gleichungssysteme beschreiben kann und damit ihre Gleichgewichte findet, treten im andern Fall häufig Differentialgleichungen auf oder wenigstens differentielle Betrachtungsweisen, die einen höheren mathematischen Aufwand erforderlich machen. Damit bewegt man sich dann immer noch im Bereich der determinierten Systeme.
Die Mehrzahl der Systeme wird allerdings so beschaffen sein, dass man einerseits eine ungeheuer große Zahl von Zuständen vor sich hat, andererseits aber oft nicht genau festlegen kann, welcher Zustand von einem gegebenen Zustand aus als nächster erreicht wird. Man kennt dann nur die Wahrscheinlichkeit, mit der von einem bestimmten Zustand ans jeder andere erreicht wird. Solche Maschinen sind nicht mehr determiniert, sondern stochastisch. Zu ihrer Beschreibung benötigt man die Wahrscheinlichkeitsrechnung - etwa in Form von Korrelations- und Varianzrechnungen.
Der Übergang vom stochastischen zum deterministischen System ist gelegentlich möglich, und zwar dann, wenn die eingetragenen Wahrscheinlichkeiten nahe bei Null und Eins liegen. Man rundet dann auf Eins auf und Null ab, je nach Gegebenheit, und erhält ein zwar nicht ganz scharfes, dafür aber deterministisches Modell. Denn selbstredend sind sowohl die Übergangsmatrizen als auch die zugehörigen Graphen Modelle für Systeme.
Die Zahlen in einer Übergangsmatrix haben einen inneren Zusammenhang, wie man das am Beispiel für das System "Ameisenhaufen" sieht. Die Matrix spiegelt das statistische Verhalten der Ameisen wider, und zwar nach drei geographischen Zuständen (Zone A, Zone B und Zone C), die alle gleichzeitig bestehen. Von je hundert Ameisen in Zone A verbleiben 70 in A und 30 wandern nach B. Von A nach C wandert keine, weil sie dabei ja durch B hindurchmuss und deshalb in Spalte B erscheint. Würde ein unterirdischer Gang von A nach C führen, dann hätte man auch im Kreuzungspunkt von A nach C einen von Null verschiedenen Wert. Dies ginge allerdings zu Lasten der Ameisen, die in A bleiben oder nach C gehen.
Die Summe der Ameisen in jeder Spalte muss stets hundert sein. Sind es weniger, dann hat der Ameisenhaufen Schwund - etwa durch einen Ameisenbär. Sind es irgendwo mehr als hundert, dann kommen offenbar neue Ameisen zur Welt. Wenn wir beides ausschließen, müssen die Summen in den Zeilen und Spalten 100 sein, wenn wir von Prozenten reden, und 1, wenn wir es mit Wahrscheinlichkeiten zu tun haben.
Die Matrix ist außerdem symmetrisch zu ihrer Hauptdiagonalen. Wäre dies nicht der Fall, so hätten wir es mit einer Verschiebung der Ameisen zu tun - etwa wenn der Ameisenhaufen in Unruhe gerät, weil er von außen gereizt wird.
Unsere Matrix ist ein Schnappschuß. Die Werte auf den Kreuzungspunkten sind eigentlich Funktionen der Zeit. Wir haben es offenbar mit einer zeitlich veränderlichen, dynamischen Struktur zu tun. Damit stellt die Übergangsmatrix zugleich das allgemeine Modell für ein stochastisch/deterministisches und statisch/dynamisches System dar. Dies zeigt auch folgende Tabelle: