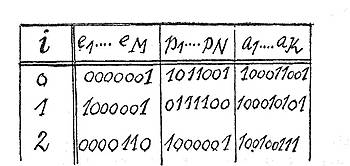
Die Theorie der Automaten ist eine recht abstrakte Disziplin, die wir hier nur grob skizzieren können. Man geht davon aus, dass der Automat im Innern bestimmte Zustände annehmen kann. Schalter sind geschlossen oder offen, Transistoren führen Strom oder nicht und so weiter. Diese Zustände kann man mit beliebigen Zeichen benennen. Wir wollen jedoch nur Nullen und Einsen zur Darstellung heranziehen, was bedeuten soll, dass ein bestimmter Zustand entweder da ist oder nicht. Jeder Zustand ist also eine Variable p, die den Wert 0 oder 1 annehmen kann. Alle N Zustände sind die Variablen p₁ bis p_N.
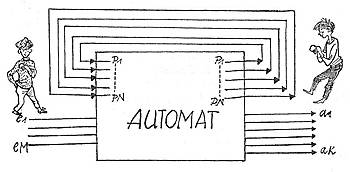
In einen Automaten führen Kanäle hinein. Wir nehmen auch hier an, dass diese durch die M binären Variablen e₁ bis e_M dargestellt werden, die auch wieder nur die Werte Null und Eins annehmen können. Ebenso gibt es K Ausgangsvariablen a₁ bis a_K.
Die Verhältnisse werden nun so liegen, dass die Zustände des Automaten durch die bestimmten Werte Null und Eins für jede Variable, sei sie nun Eingangsvariable, innere Variable oder Ausgangsvariable, charakterisiert sind. Die Eigenschaft, Automat zu sein, kommt dadurch zum Ausdruck, dass sich diese Kette von Werten laufend ändert, und zwar fortschreitend in der Zeit. Wir können uns darauf beschränken, für jeden Zeitpunkt anzugeben, welchen Zustand der Automat hat. Wir ordnen dies, beginnend bei Null, so an, dass aufeinanderfolgende Zustände auch auseinander hervorgehen.
Was wir hier beschreiben, ist ein endlicher Automat mit diskreten Schritten. Die Darstellung ist verwandt mit der bereits gezeigten Übergangsmatrix. Es handelt sich bei dieser Darstellung um streng determinierte Automaten. (Stochastische Automaten müssen so aussehen, dass eine stochastische Funktion angibt, mit welcher Wahrscheinlichkeit die einzelnen Zustandsbeschreibungen aufeinander folgen; man kann sie dann nicht mehr einfach anordnen und aus der Reihenfolge schließen, dass Zustände des Automaten auseinander hervorgehen.) Es sei noch darauf hingewiesen, dass der Automat keineswegs in zeitlich gleichen Abständen arbeiten muss. Es kann sehr wohl sein, dass der Übergang von Zeile 5 nach Zeile 6 länger dauert als der von Zeile 8 nach Zeile 9. Eine Tabelle für einen solchen Automaten sieht folgendermaßen aus:

Bildlich stellt man das so dar:

Der Kasten leistet dabei die Verknüpfung. Wie er das macht, wie man das realisiert, führt jeweils auf einen zu dieser Struktur isomorphen realen Automaten, auf eine existierende Maschine.
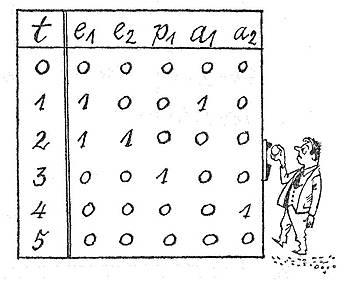
Für einen ganz einfachen Automaten, der eine Ware abgibt, sieht dies so aus: Wir haben einen Schlitz, in den Geld eingeworfen wird.
Ist das Geld in Ordnung, so wird die Eingangsvariable e₁ zu 1
gesetzt. Im andern Fall hat sie den Wert 0. Darauf muss man durch Drücken eines Knopfes die Ware anfordern. Dies ist e₂. Ist e₂ = 0, so heißt das: "Ware nicht angefordert." Wenn Geld eingeworfen ist, leuchtet eine Lampe a₁ auf (a₁ = 1), die ein Feld beleuchtet, in dem "Bitte Knopf drücken" steht. Wenn der Knopf gedrückt ist, wird ein Raster freigegeben (p₁= 1), das bewirkt, dass die Ware abgegeben wird. Sie fällt in das Ausgabefach (a₂ = l). Dann gehen alle Variablen auf Null und warten, bis wieder jemand Geld einwirft. Daraus ergibt sich folgende Automatentafel:

Wie man sieht, ist zum Zeitpunkt 3 der Automat mit sich selbst beschäftigt, die Auslieferung der Ware zu bewerkstelligen, Zustand 5 des Automaten ist mit Zustand 0 identisch, der Automat hat also ein einseitig zyklisches Verhalten.
Sehr zu Recht vermerkt H. Anschütz in seiner Darstellung der mathematischen Kybernetik "Kybernetik - kurz und bündig" (Würzburg 1967) : "Auch ist das Wort Automat (z. B. Zigarettenautomat) vorbelastet. Weil es weiterhin primitive Automaten gibt, die immer dieselbe Arbeit in ständiger Wiederholung exakt und gleichförmig durchführen, ruft das Wort "Automat" im naiven Sinne auch die Vorstellung des Einförmigen, Monotonen, immer exakt Gleichen hervor. Es sind sogar relativ leicht Automaten konstruierbar, die in einer vorgegebenem Lage willkürliche Entscheidungen treffen können."
Wir brauchen unseren Leser nur an das Stichwort "Markoff-Maschine" und an den stochastischen Prozeß zu erinnern, um ihm dieses Zitat verständlich zu machen.
Auch Computer lassen sich mit Automatentafeln beschreiben, und sie werden damit beschrieben. Allerdings sind die Tafeln für so komplexe Gebilde nicht mehr mit der primitiven Tafel unseres Warenautomaten zu vergleichen. Die höhere Automatentheorie befaßt sich vor allem mit dem Problem - und dies ist ein typisch kybernetisches Problem -, Schaltwerke zu finden, deren Verhalten durch eine bestimmte Tafel wiedergegeben wird. Dabei muss man beachten, dass Schaltwerke mehr sind als die Schaltungen der Booleschen Algebra. In den Schaltwerken tritt noch die Zeit auf.
Der Unterschied zwischen einem durch Boolesche Algebra beschriebenen Sachverhalt und einem, zu dessen Darstellung ein Schaltwerk benötigt wird, ist der zwischen einem statischen und einem dynamischen System. Die Frage, ob man alle dynamischen Systeme mit Schaltwerken simulieren, also durch Tafeln darstellen kann, ist offen. Sie enthält zugleich die Frage, ob man das menschliche Verhalten durch eine solche Automatentafel vollständig beschreiben kann.
Eine kurzgefaßte Darstellung der Automatentheorie (sowie der mathematischen Kybernetik überhaupt) findet sich in dem obengenannten Buch von H. Anschütz, "Kybernetik kurz und bündig", das allerdings kein Lehrbuch ist und mathematische Kenntnisse voraussetzt.