Wie man sieht, kann man insgesamt 16 solcher Verknüpfungen finden, von denen aber nur einige wesentlich sind. Wichtiger ist die sogenannte Negation, die man mit dem Symbol N charakterisiert.
Ist q falsch, so ist Nq wahr; ist q wahr, so ist Nq falsch. Solchermaßen kann man für die Beschreibung logischer Aussagensysteme eine eigene Algebra aufbauen, die man Aussagenlogik nennt. Sie wurde von George Boole entwickelt und heißt deshalb auch Boolesche Algebra. Eine knappe Darstellung des Aussagenkalküls findet der Leser in dem wissenschaftlichen Werk von Hilbert-Ackermann, "Grundzüge der theoretischen Logik", 4. Auflage, 1959.
Die Boolesche Algebra ist deshalb interessant, weil sie zugleich die Basis für die Berechnung von Schaltungen ist, wie wir sie in diesem Kapitel verwendet haben. Sie ist ein sehr wichtiges Instrument beim Aufbau und bei der Konstruktion von sogenannten logischen Schaltungen, die die Grundbausteine der Elektronik (unter anderem auch der Elektronenrechner) und damit der Kybernetik sind. Sie zeigt auch, wie grundsätzlich diese Zusammenhänge unser Verständnis und die Möglichkeit zur logischen Einsicht in die uns umgebende Welt berühren.
In K. Steinbuch, "Automat und Mensch", 3, Auflage, Berlin, Heidelberg, New York 1965, findet sich eine Reihe von Beispielen über die Möglichkeiten zur technischen Interpretation der Booleschen Algebra sowie eine Übersicht über die Booleschen Verknüpfungen und ihre schaltungstechnische Realisierung - etwa mit Hilfe von Relais oder Transistoren.
In der Booleschen Algebra liegt auch der Schlüssel zum Verständnis der Funktion der elektronischen Rechenanlagen, die nach diesen Prinzipien konstruiert werden. Der Leser sei dazu auf das Buch der beiden Autoren Lohberg/Lutz, "Was denkt sich ein Elektronengehirn", Franckh'sche Verlagshandlung, 3, Auflage, Stuttgart 1966, hingewiesen, in dem ausführlich dargestellt ist, wie aus solchen Grundbausteinen ein Computer aufgebaut wird.
UND und ODER
Die hier angedeutete Möglichkeit zur schaltungstechnischen Behandlung der Begriffe UND und ODER ist nicht nur für die Kybernetik von grundsätzlicher Bedeutung. Die dazugehörige Theorie existiert seit Mitte des letzten Jahrhunderts in Form der Booleschen Algebra (George Boole, englischer Mathematiker, 1815 bis 1864), die wiederum zum Bereich der mathematischen Logik oder Logistik gehört.
Sind etwa p und q elementare, aber vollständige Aussagen (wie zum Beispiel "Das Wetter ist schön", "Die Rose ist rot"), so kann ein solcher Satz entweder wahr oder falsch sein. Codiert man wahr zu 1 und falsch zu 0, so kann die Variable p den Wert 0 oder 1 haben. Die kombinierte Aussage ("Das Wetter ist schön" UND "Die Rose ist rot") schreibt sich jetzt als
p UND q
und entsprechend gibt es ein
p ODER q.
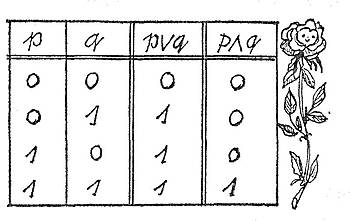
Für UND benutzt man oft das Zeichen & oder ∧ , für ODER das Zeichen ∨ (vom lateinischen vel). Die Logistik fragt, unter welchen Voraussetzungen pVq wahr oder falsch ist. Hier kann man die Antwort noch relativ einfach geben. Sicherlich ist pVq dann richtig, wenn p oder q oder beide richtig sind. Dies kann man in einer Tabelle darstellen, die auch gleich die entsprechende Eintragung für p ∧ q enthält;